 Autor: Bárbaro Frómeta Elías / barbaro.frometa@gtm.jovenclub.cu
Autor: Bárbaro Frómeta Elías / barbaro.frometa@gtm.jovenclub.cu
Resumen:
Durante el diseño y desarrollo de aplicaciones informáticas interactivas se crean rutinas que permiten detectar el choque entre partículas y definir las acciones a seguir por cada una de ellas después de la interacción (motor de colisiones o motor físico). Una de las incógnitas mayores radica en ¿cómo desarrollarlas?, aspectos que dan lugar a determinar como objetivo del presente artículo ofrecer una aproximación de cómo se crean los componentes del motor de colisiones en las aplicaciones informáticas, desde la programación gráfica en 2D. El presente artículo permite allanar el camino para la comprensión, desarrollo e implementación de productos informáticos en los que sea imprescindible el control de los eventos y de la interacción entre los objetos. En el desarrollo del mismo se emplearon como procedimientos y métodos fundamentales la observación, revisión de documentos, encuestas y modelación. A partir de un proceso de socialización e implementación del presente artículo, se consideran resultados favorables, determinado por el nivel de aceptación y comprensión por parte los usuarios interesados, por lo que se pueden considerar que el material instructivo que se propone es de vital importancia en el desarrollo de productos informáticos interactivos de multimedia.
Introducción
El desarrollo vertiginoso de las tecnologías de informática en todo el mundo se pone de manifiesto en la gran cantidad y diversidad de programas o aplicaciones informáticas que se introducen en todos los campos y sectores de la sociedad para controlar o simular procesos.
La informática se hace presente fundamentalmente en la esfera de la recreación, investigación científica y la educativa. Para cada una de ellas se implementan softwares capaces de controlar o simular la realidad material, a partir de una concepción virtual. Dos de esos tipos de aplicaciones son los videojuegos y los simuladores. El primero de ellos, arraigado en la sociedad moderna y ampliamente distribuido en todo el mundo, el segundo tipo de aplicación clasifica dentro del software educativo y es capaz de trasmitir información a través de modelos que simulan procesos que ocurren en la realidad material lo que permite un alto nivel de interactividad.
Al observar el funcionamiento de algunos de esos programas informáticos, notamos la presencia, casi en su totalidad, de componentes gráficos (objetos virtuales) que interactúan mutuamente y que al ponerse en contacto responden bajo una acción, de acuerdo a determinadas características. La parte de la aplicación que controla esos eventos se denomina Motor de impacto o motor de colisiones.
En Cuba se ha difundido e incentivado el uso de las tecnologías informáticas, a partir de la creación de centros dedicados a esa actividad, en los que se destacan la fundación del movimiento de Joven Club, creado en 1987, y la Universidad de Ciencias Informáticas; ambas instituciones ideadas por el líder de la Revolución Cubana Fidel Castro Ruz.
Una de las prioridades dentro de los programas de estudio en los Joven Club de Computación está relacionada con la materia de programación, en lo que se incluye la programación gráfica. A pesar de los notables avances en la difusión, masificación de la informática, y las incursiones en el desarrollo de aplicaciones como videojuegos, simuladores y otros en los que están presentes los componentes gráficos, persisten algunas problemáticas que limitan su total desarrollo, esas problemáticas incluyen: poco conocimiento de la relación entre la geometría analítica y los elementos gráficos tanto estáticos como dinámicos, presentes en las aplicaciones informáticas, así como el insuficiente conocimiento sobre el funcionamiento de un motor de colisiones en las aplicaciones informáticas.
Las situaciones problémicas definidas dan lugar a concebir como objetivo del presente artículo ofrecer una aproximación de cómo se implementa el motor de colisiones en las aplicaciones informáticas a través de la programación gráfica. Considerándose como aporte fundamental, un material instructivo que permite allanar el camino para la comprensión, producción e implementación de productos informáticos en los que sea necesario el control a través de un motor de colisiones.
Desarrollo
Esta investigación está sustentada sobre la base de la utilización del método científico sistémico para su realización. “El método sistémico está dirigido a estudiar el objeto mediante la determinación de sus componentes, así como la relación entre ellos” [14]. Este método permitió dividir el proceso de desarrollo de la investigación en dos elementos fundamentales, con el objetivo de analizar cada tema y lograr un dominio profundo de los mismos. Estos elementos son los conceptos de detector de colisiones y conductor de evento (driver).
Motor de colisiones
El motor de colisiones (también llamado motor físico o de impacto) puede estar formado por más de un elemento, en dependencia de su complejidad y finalidad. La separación en partes distintas permite individualizar y dinamizar su uso, así como el diseño y mantenimiento. Para el motor de colisiones es imprescindible contar con dos elementos o subconjunto; el detector de impacto y el conductor de eventos.
Durante la definición del concepto de Motor de colisiones se destacan los criterios de diferentes autores que tratan el tema desde diferentes puntos de vistas. Según la definición expuesta en Wikipedia, define el motor de videojuegos como elemento contenedor del detector de colisiones de la siguiente forma: Un motor de videojuego es un término que hace referencia a una serie de rutinas de programación que permiten el diseño, la creación y la representación de un videojuego [2]. Al considerar que se ha publicado poco sobre este tema, asumimos el concepto del detector de colisiones, el cual forma parte del motor físico o de colisiones como un conjunto de rutinas que determinan la forma de interacción entre dos objetos virtuales, encargado de detectar cuando se ponen en contacto. De lo anterior, también se puede inferir el concepto de conductor de eventos como un conjunto de rutinas que definen la actitud a tomar por dos objetos virtuales luego de la interacción (choque) bajo determinadas condiciones.
En los videojuegos, simulador, entrenadores u otro tipo de aplicación expresados tanto en 2D o en 3D, las animaciones están conformadas por fotogramas que se muestran una a una de forma continua o selectiva, dando lugar a la representación del evento, en el que se destaca el movimiento relativo de los objetos virtuales que interactúan entre sí de forma individual o en masa. Cada evento es controlado por el conductor de eventos (driver), convirtiéndose en la herramienta que media entre el usuario y la aplicación, razones por la cual, durante el diseño se debe atender a dos eventos; el choque (colisión bajo la acción) y la reacción después del choque.
Detector de colisiones
Se emplea el término de colisión para representar la situación en la que dos o más partículas interaccionan durante un tiempo muy corto. Se supone que las fuerzas impulsivas debidas a la colisión son mucho más grandes que cualquier otra fuerza externa presente [11].
La colisión entre objetos virtuales (Sprites) es frecuente durante el funcionamiento de los videojuegos u otro tipo de modelos informáticos. En dependencia de la geometría de los objetos interactuantes, ésta se produce en uno o varios puntos a la vez, los cuales deben determinarse con precisión para acercarse en lo posible a la realidad material.
El diseño de un detector de colisiones involucra fundamentalmente cálculos de posicionamientos geométricos, si se tiene en cuenta que por lo general los objetos virtuales se conforman por elementos geométricos en el espacio y el plano, por lo que la detección de la colisión puede ser de dos tipos:
- Por Área: los objetos ocupan un área, rectangular o circular; cuando dos de estas áreas se superponen hay una colisión.
- Pixel a Pixel: los objetos ocupan un área rectangular, pero tienen una máscara que define qué píxeles son visibles.
- DETECCIÓN DE COLISIONES POR ÁREA
Debemos recordar que la programación que involucre imágenes debe hacerse a través de un objeto denominado Timágen, presente en las plataformas de programación. Ese objeto se enmarca en un rectángulo, independientemente de la forma y su propiedad picture (imagen conformada por mapabit), toda picture se encuadra dentro de un rectángulo, y puede estar representado por las figuras geométricas básicas (triángulo, rectángulo, círculo) o por un polígono irregular.
PRIMER CASO: Los objetos interactuantes son figuras rectangulares (fig.1)
Las figuras rectangulares que se ponen en contacto lo hacen a través de sus lados. En este caso es muy cómodo hacer coincidir el área de la imagen con el rectángulo contenedor de la imagen, de esta manera cuando hacemos referencia a las dimensiones de la imagen, se refiere a la dimensiones del objeto contenedor (Timage).
Ancho del objeto imagen = ancho de su bitmap
Alto del objeto imagen = alto de su bitmap
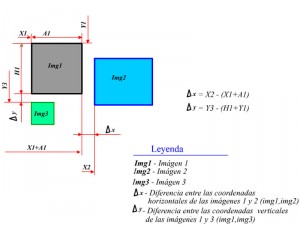
Para detectar la colisión entre objetos rectangulares basta tener en cuenta las coordenadas de los lados en contacto.
∆x = Img2.x2 – (Img1.x1 + img1.ancho)
Si ∆x <= 0 entonces hay colisión.
Si ∆x > 0 entonces no hay colisión.
En caso de que la colisión se produzca por la coordenada vertical, la referencia será con respecto a ∆y
∆y = Img3.y3 – (Img1.y1+ img1.alto).
SEGUNDO CASO: las imágenes interactuantes son circulares (fig.2).
Recordemos que todo mapabit se circunscribe en un objeto Timagen rectangular, que es en realidad el cuadrado asociado a una circunferencia, la cual coincide con el diámetro del círculo. En este caso se hace coincidir el círculo con las dimensiones del objeto Timagen y se asume un color de fondo preferentemente blanco para enmascarar los píxeles del fondo que lo convierte en trasparente. Esas condiciones permitirán detectar la colisión a través de los cálculos geométricos, en dependencia de la posición relativa de ambas esferas, por lo que analizaremos el choque en dos condiciones posibles.
- Los ejes de ambas esferas coinciden
Si el eje de ambas esferas coinciden (tanto en la vertical como en la horizontal) eso implica que el choque se producirá por el extremo de ambas esferas, por lo que la detección del choque se determina primero por el área rectangular y luego por el área circular, al coincidir el extremo de la esfera con el borde del rectángulo contenedor, el cálculo debe detectar el choque por cualesquiera de sus lados. Solo basta con comparar la posición relativa de ambos rectángulos.
- Los ejes de ambas esferas no coinciden
Cuando los ejes de ambas esferas no coinciden, el choque se produce en forma tangencial. En estas condiciones se genera un triángulo rectángulo entre el centro de ambos círculos y los ejes horizontales y verticales, produciéndose el contacto a través del lado h (hipotenusa) en el punto Pc (fig. 2).
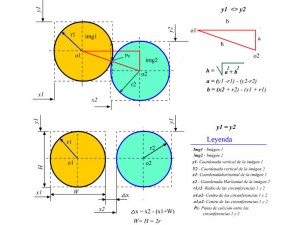
SI y1 <> y2: Si h <= r1+r2 indica que hay colisión, en caso contrario no hay colisión
Si y1 = y2 : ∆X <= 0 indica que hay colisión, en caso contrario no hay colisión
TERCER CASO: colisión entre dos figuras triangulares.
En este caso colisionan dos figuras triangulares inscriptas en un rectángulo del objeto Timagen, cuya altura coincide con la altura del triángulo y el ancho coincide con la base del triángulo, por lo que los puntos de colisión se determinan a través de las coordenadas, el ancho y la altura de ambas imágenes.
– Si la colisión se produce de borde a borde de ambas figuras o de borde a la base, entonces la detección se determina por el área rectangular del objeto.
– Si la colisión se produce desde el borde y el área oblicua, entonces la detección de la colisión se determina a través de cálculo geométrico (fig. 3)
Como la colisión se produce en el punto F’, F, basta determinar las dimensiones de los segmentos F’F y FA.
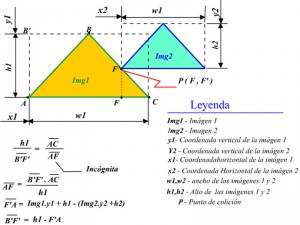
Fig.3: Colisión entre dos figuras triangulares
Como se aprecia en la fig. # 3, si x1 + af <= x2 entonces hay colisión.
CUARTO CASO: la colisión se produce entre un objeto triangular y un objeto circular.
En este ejemplo analizaremos dos posibilidades:
- El movimiento de la esfera es perpendicular al lado C, en este caso la colisión se producirá en el punto p1’(n’, m’) del triángulo, con el punto de colisión p1 de la esfera , perfectamente determinable.
El movimiento de la esfera es perpendicular a la base del triángulo: en este caso la colisión debe producirse en el punto donde coincide el punto de colisión del círculo p2(f, z), con el punto de colisión del triángulo p1(n,m)). El triángulo tiene ángulo de inclinación conocido o por lo menos determinable a través de las dimensiones conocidas ancho (a) y alto (h2) del objeto contenedor del triángulo (Timage).
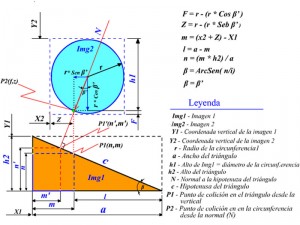
Fig. 4: Colisión entre un objeto circular y uno triangular.
En la figura 4 se observa que ambas imágenes están separadas, por lo que es necesario determinar a priori en qué punto colisionarán.
Debemos partir que el punto (p2) de colisión para la circunferencia se determina por la perpendicular al plano inclinado (normal al plano inclinado), el cual pasa por su centro, formando un ángulo β con la vertical, dando lugar a un triángulo rectángulo, cuyos catetos son r x cos β y r x sen β. Por esas razones entre otras, el ángulo que se forma entre la vertical y la perpendicular al plano inclinado (β’) es igual al ángulo del triángulo (β), o sea β = β’, según la teoría geométrica de correspondencia de ángulo. [8 ]
La esfera colisionará con el plano inclinado cuando las coordenadas de los puntos p1 y p2 sean iguales (P1 = p2, p1’=p2), esto puede ocurrir a partir de dos variantes: una si el movimiento de la esfera es perpendicular al plano inclinado (hipotenusa del triángulo), la otra si el movimiento de la esfera es perpendicular a la base (a) del triángulo las coordenadas de p1 y p2 están dado por los vectores P1(n, m) y P2(f, z).
¿Cómo calcular esas coordenadas? Recordamos que los objetos virtuales en las plataformas de programación tienen las siguientes propiedades: alto (height), ancho (width) y las coordenadas izquierda (left) y derecha (right), por lo que para los objetos anteriores basta con encuadrarlo en su rectángulo contenedor y conocerá la altura, y ancho del triángulo, así como el diámetro del círculo, en lo adelante solo basta un poco de la metodología de cálculo de las coordenadas como se muestra en la figura 4
Si las coordenadas de p1 = Coordenadas de p2 indica que hay colisión.
Conclusiones generales
Los aspectos anteriormente elaborados permiten ofrecer las siguientes conclusiones generales:
- Se ha escrito poco sobre la metodología del diseño de las rutinas que componen el motor de colisiones o motor físico, si bien es cierto que para cada producto se diseñan motores de colisiones diferentes, persiguen el mismo objetivo.
- El motor de colisiones es una herramienta indispensable para el desarrollo de modelos informáticos por lo que su implementación debe ser lo más precisa posible.
- La geometría analítica guarda una estrecha relación con la programación gráfica, al igual que la física con el diseño de herramientas y modelos que represente la realidad material y el movimiento de los cuerpos.
BIBLIOGRAFÍA
1- Sitio Web Colectivo de autores (2010), blog educarchile Ley de conservación del momentum lineal. Consultado el 4 de septiembre de 2013. Disponible en: http://www.educarchile.cl/ech/pro/app/detalle?ID=133119.
2- Sitio Web: Colectivo de autores (2009) Blog.Wikipedia: motor de videojuegos. Consultado el 4 de septiembre de 2013. Disponible en: http://www.wikipedia.org/wiki/Motor_de_videojuego.
3- Sitio Web: Ruiz, Juan K. (2007), Blog juank.black-byte: Detección de Colisiones 2D básica .Consultado el 9 de octubre de 2013. Disponible en: http://juank.black-byte.com/xna-colisiones-2d/.
4- Sitio Web: Colectivo de autores (2010), Blog Xuletas : cantidad de movimiento: impulso y choque .Consultado el 9 de octubre de 2013. Disponible en: http://www.xuletas.es/ficha/impulso-y-choques/.
5- Sitio Web: Colectivo de autores (2008) Blob fing.edu: Computación Gráfica Avanzada. Consultado el 20 de octubre de 2013. Disponible en: ww.fing.edu.uy/inco/cursos/cga/Clases/…/Detecciondecolisiones.pdf.
6- Sitio Web: García, Angel F. (2010), Blog sc.ehu: choque en una dimensión. Consultado el 12 de octubre de 2013. Disponible en: http://www.sc.ehu.es/sbweb/fisica/dinamica/con_mlineal/choques/choques.htm.
7- Sitio Web: colectivo de autores (2010). Blog. Ecured: geometría plana. Consultado el 11 de octubre de 2013. Disponible en: http://www.ecured.cu/index.php/Geometr%C3 %ADa_Plana#Transversales
8- Sitio Web: Yosvanys,Escobar, Vázquez (2012) .blog Ecured: semejanza geométrica en triángulos. Consultado el 11 de octubre de 2013. Disponible en: http://www.ecured.cu/index.php/Semejanza_geom%C3%A9trica_en_tri%C3%A1ngulo.
9- Sitio Web: Wallace, R, E.(1988), pp. 815-819. Blog: choque de bolas de villar. Consultado el 16 de octubre de 2013. Disponible en: www.sc.ehu.es/sbweb/fisica/solido/mov_general/choque/choque.htm.
10- Sitio Web: Terrel, Pérez, Walter (2010).Blog.slideshare: Choque en dos dimensiones. Consultado el 16 de octubre de 2013. Disponible en: http://www.slideshare.net/walterperezterrel/semana-15-choque-en-dos-dimensiones-unac-2009-b.
11- Sitio Web: Terrel, Pérez, Walter (2010).Blog.slideshare: Choque en dos dimensiones. Consultado el 16 de octubre de 2013. Disponible en: http://www.slideshare.net/walterperezterrel/semana-15-choque-en-dos-dimensiones-unac-2009-b.
12- Sitio Web: Colectivo de autores (2009) Blog.Wikipedia: Choque. Consultado el 4 de septiembre de 2013. Disponible en: http://es.wikipedia.org/wiki/Choque_%28f%C3%ADsica%29.
13- Sitio Web: Colectivo de autores (2009) Blog.Wikipedia: Colisión. Consultado el 1 de octubre de 2013. Disponible en: http://www.slideshare.net/anthonygui/choque-o-colisiones-de-la-fisica.
Hernández León Rolando Alfredo, Coello González Sayda (noviembre 2002), El paradigma cuantitativo de la investigación científica. Página 85.

