Autor: Ing. Judiel Reyes Aguilar / supervc@cenit.cult.cu
Coautores: Ing. Glenda Beatriz Guzmán Paz, Dr. Vitalio Alfonso Reguera
Resumen: Uno de los principales problemas asociados a las redes de sensores inalámbricos es cómo hacer un uso eficiente de la energía disponible. Con el objetivo de conseguir un menor gasto energético en estas redes es conveniente aplicar la Codificación de Fuente Distribuida para reducir la cantidad de información a transmitir. Esta técnica se refiere a la compresión separada y la descompresión conjunta de fuentes mutuamente correlacionadas. El presente artículo hace una revisión bibliográfica sobre la aplicación y despliegue de la Codificación de Fuentes Distribuida en las redes de sensores inalámbricos. En un primer momento se analizan los fundamentos teóricos de este método de codificación y finalmente se repasan los principales principios dados por la literatura para su utilización en las redes de sensores.
Palabras Clave: Codificación de Fuente Distribuida, Redes de Sensores, estrategia simétrica, estrategia asimétrica
Abstract: One of the principal problems related to wireless sensor networks is about how to do an efficient use of available energy. In order to get a lower energy expenditure, in these networks should be applied the Distributed Source Coding to reduce the amount of information to be transmitted. This technique refers to the separate compression and decompression joint mutually correlated sources. This article makes a literature review on the implementation and deployment of distributed source coding in wireless sensor networks. At first moment the theoretical foundations of this coding method are analyzed and finally the main principles given in the literature for use in sensor networks are reviewed.
KeyWords: Distributed Source Coding, sensor networks, symmetric strategy, asymmetric strategy
Introducción
Una de las aplicaciones de la ingeniería más investigada en los últimos años es las redes de sensores. Estas redes despliegan pequeños dispositivos llamados nodos, interconectados entre sí de forma inalámbrica, sobre un área geográfica para el monitoreo de fenómenos físicos. Los nodos sensores son capaces de captar, procesar y transmitir información extraída de áreas físicas de observación, al resto de los nodos de la red (Dargie & Poellabauer, 2010). Actualmente estas redes se emplean en diversos campos de la ciencia, tales como: monitoreo de un hábitat; detección de incendios, terremotos o inundaciones; edificios “inteligentes”; control de tráfico y asistencia militar o civil; entre otros.
Típicamente un nodo sensor es un dispositivo diminuto que incluye tres componentes básicos: un subsistema de sensor para la adquisición de los datos del ambiente físico circundante, un subsistema de procesamiento y almacenamiento local de los datos; y un subsistema de comunicación inalámbrico para trasmitir y recibir sus datos y los de otros nodos vecinos. Además de estos componentes, una fuente eléctrica abastece la energía requerida para que los dispositivos realicen las tareas necesarias. Esta fuente a menudo consiste en una batería con limitado presupuesto de energía.
En ocasiones puede ser imposible o inconveniente cambiar las baterías, porque los nodos pueden estar desplegados en un ambiente hostil o las funciones que realice la red no lo permitan. Es decir que, las redes de sensores deben tener un largo tiempo de vida, suficiente para cumplir las aplicaciones requeridas. En muchos casos este tiempo de vida se extiende por varios meses y años. Por lo que un requisito imprescindible en el diseño de los nodos y el modelo de red es la optimización de la energía y la maximización de su tiempo de vida.
En muchos escenarios de las redes de sensores se logra una alta correlación espacial entre los datos captados por los nodos. Una consecuencia de esta correlación es que las lecturas entre nodos vecinos son altamente redundantes. Explotar esta correlación para remover los datos redundantes a través de una técnica de compresión, permite reducir los bits a trasmitir y de esta forma reducir la energía consumida en el proceso de trasmisión de los datos.
Las investigaciones han demostrado que aproximadamente el 80 % del consumo de energía de cada nodo es usado en la trasmisión de los datos. Lo que indica que el uso de técnicas de compresión, que minimice el tamaño de los datos a trasmitir, es imprescindible en la optimización energética en la red. Sin embargo, las restricciones de la energía limitan la capacidad de procesamiento y la potencia de trasmisión de los nodos. Por otra parte, el impacto del ruido involucrado por el uso de canales inalámbricos dificulta la reconstrucción de los datos. Por lo que, para enviar los datos recolectados por los sensores a la estación base, se requiere buscar métodos robustos con alta compresión y baja complejidad, que permita una trasmisión de los datos eficiente en el ahorro de energía (Xiong, Liveris, & Cheng, 2004).
Esta compresión puede alcanzase convencionalmente con un método de codificación de fuente si se conoce la redundancia entre los datos. Sin embargo esto requeriría comunicación entre los nodos previamente antes de iniciar el proceso de codificación lo cual no sería permisible por las restricciones energéticas dadas en la redes de sensores. Sorprendentemente en 1973, Slepian y Wolf (1973) demostraron que cuando las fuentes están correlacionadas la comunicación entre los codificadores no es necesaria para lograr la compresión de los datos, siempre que estos se decodifiquen en conjunto, dando las primeras nociones de la Codificación de Fuente Distribuida.
La Codificación de Fuente Distribuida se refiere a la compresión separada y descompresión conjunta de dos o más fuentes físicamente separadas (de aquí el termino de distribuido) en los codificadores y decodificadas en conjunto en el decodificador. La Codificación de Fuente Distribuida es de esta forma un método de codificación que tiene como objetivo explotar las dependencias mutuas a través de diferentes fuentes que requieren no tener comunicación entre sí (Stankovic, Stankovic & Cheng, 2010).
La Codificación de Fuente Distribuida aparece como un problema de la Teoría de la Información, en este artículo Slepian y Wolf estudiaron el simple caso de la Codificación de Fuente Distribuida con dos fuentes discretas que son comprimidas independientemente y decodificadas sin pérdidas en el decodificador de forma conjunta, y determinaron una región para las razones de compresión alcanzable, demostrando que la codificación por separado es tan buena como la que se puede realizar en conjunto. Este resultado provocó una gran cantidad de investigaciones sobre la Teoría de Información, esfuerzos que resultaron en varias extensiones de este trabajo (1973).
Desde finales de la década de los 70, con los estudios de Wyner (1978) se demostró que era posible la realización de la Codificación de Fuente Distribuida usando códigos de canal, pero debido a la carencia de aplicaciones potenciales, el estudio del diseño de un código empezó solo a finales del pasado siglo. El lanzamiento de las redes de sensores retomo los estudios en este campo. El primer diseño practico se reportó en el 2000 en (Pradhan & Ramchandran, 2000, 2003).
En los años posteriores se han desarrollados códigos más potentes. Los estudios más reciente sobre la Codificación de Fuentes Distribuida investigan como desplegar de la forma más óptima esta técnica de compresión en las redes de sensores (Abughalieh, Steenhaut, Lemmens & Nowé, 2012; Arjmandi & Lahouti, 2011; Arjmandi, Taki & Lahouti, 2011) y otras aplicaciones como la codificación distribuida de video (Tubaro & Vetro, 2013). Actualmente se analiza como interactúa esta técnica de compresión con otras capas de red como el enrutamiento (Li & Ramamoorthy, 2011) y el control de acceso al medio.
El presente artículo hace una revisión bibliográfica sobre la aplicación y despliegue de la Codificación de Fuentes Distribuida en las redes de sensores inalámbricos. En un primer momento se analizan los fundamentos teóricos de este método de codificación y finalmente se repasan los principales principios dados por la literatura para su utilización en las redes de sensores.
Desarrollo
Según la teoría de la codificación de Shannon, para una fuente aleatoria X, una razón R ≥ H(x) es suficiente para trasmitir X sobro un canal confiable hasta la estación base. Por lo que, si tenemos dos fuentes (X,Y) distribuidas idénticas e independientes, y son codificadas de forma separada, se requiere que la razón total R = Rx + Ry ≥ H(X) + H(Y). Siendo Rx y Ry la razón de codificación de las fuentes X y Y, respectivamente, y H(X) y H(Y) sus entropías.
Aplicando una codificación distribuida de manera conjunta las fuentes pueden ser codificadas a razones iguales que la entropía condicional de las fuentes. Esto requeriría de comunicación entre los nodos, lo cual implica una sobrecarga adicional en la red y el objetivo de la codificación en las redes de sensores es exactamente el contrario, reducir la cantidad de procesamiento de información y por consiguiente el consumo de energía.
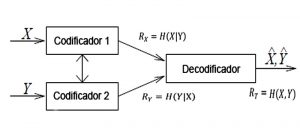
Sin embargo Slepian y Wolf demuestran que la codificación distribuida se puede lograr sin comunicación entre las fuentes siempre que estas estén correlacionas entre sí. De menara que, aplicando esta teoría, como se muestra en la Figura 1, una razón total de R = Rx + Ry ≥ H(X,Y) es suficiente, incluso si las dos fuentes son codificadas de forma separada, siempre que los datos sean descodificados de forma conjunta. Donde H(X,Y) hace referencia a la entropía conjunta de ambas fuentes (1973).
De esta manera, Slepian-Wolf demostraron que dos fuentes X y Y pueden ser descodificadas sin pérdidas siempre que cumplan con la ecuación (1).
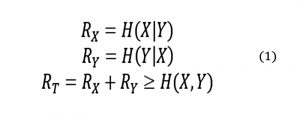
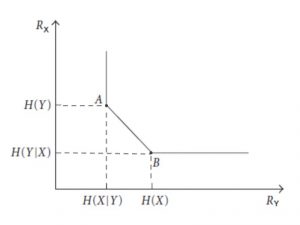
En la ecuación (1) Rx y Ry son las razones usadas para la compresión de X y Y respectivamente. Estas ecuaciones, son conocidas como la región de la codificación de Slepian-Wolf, la cual es representada en la Figura 2, y muestran que la razón total puede ser tan pequeña como la entropía conjunta de las fuentes, lo cual es lo mismo que la fuente codificadas en conjunto. A partir de esta región se han planteado dos estrategias de codificación: la asimétrica y la simétrica.
El caso asimétrico, correspondiente a los puntos A y B de la Figura 2, es cuando una de las fuentes, por ejemplo Y, es conocida sin codificar por el decodificador. Entonces una razón no mayor que H(X|Y) es suficiente para comprimir X. Aunque en el caso asimétrico es donde se logra una mayor compresión, este enfoque puede no ser aconsejable para algunas aplicaciones en las redes de sensores ya que requeriría tener disponible un nodo que brinde sus datos sin codificar, para poder decodificar la información del resto de los nodos, lo cual crearía un deválense en la energía de la red pues algunos nodos tendrían un mayor consumo que otros.
Dos soluciones se han planteado a este problema, la primera consiste en intercambiar periódicamente el rol de los nodos, de manera que la responsabilidad de actuar como información lateral no recaiga solo en un nodo sino que se remplace cada cierto tiempo. La segunda solución consiste en utilizar una estrategia simétrica. Este caso se refiere a cualquier punto en la línea entre los puntos A y B de la Figura 2. En este enfoque ambas fuentes son codificadas a una razón Rx ≥ H(X|Y) y Ry ≥ H(Y|X) , siempre que se cumpla que Rx + Ry ≥ H(X,Y), de manera que los datos codificados de ambas fuentes son decodificados de forma conjunta.
Para una mayor comprensión del teorema de Slepian-Wolf se toma como referencia un caso asimétrico, donde Y actúa como información lateral en el decodificador. La codificación verdadera se realizará en X. El codificador va a descomponer la secuencia X en el par (X1,X2) y va a codificar solo X1 con Rx bits, descartando X2. Luego el decodificador debe determinar X2, con una pequeña probabilidad de error, utilizando la correlación entre X2 y Y.
Para lograr la compresión un principio fundamental es determinar un modelo de correlación común entre los datos. La correlación entre dos fuentes puede ser modelada como un canal de correlación virtual donde X es la entrada y Y es la salida del canal (como se muestra en la Figura 3). El canal es descrito como la probabilidad de error p, la cual se define como la probabilidad de que X sea diferente de Y. De esta manera una probabilidad p está dada por una alta correlación, lo que hace posible la codificación con una razón baja. La correlación es por lo general modelada, en la literatura, como un canal virtual simétrico binario (BSC) o un canal con ruido gaussiano blanco (AWGN).
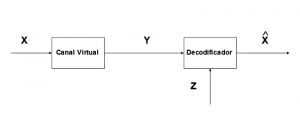
Debido a esto en la literatura se sugiere usar los principios de codificación de canal para implementar la codificación de la fuente. Esto fue sugerido por primera vez por Wyner en (Wyner, 1978; Aaron D Wyner & Jacob Ziv, 1976). La idea general es que de la misma forma que la codificación del canal expande la razón para proteger la señal de los ruidos del canal, se puede usar de forma opuesta para reducir la razón de forma controlada. La técnica se basa en un proceso llamado binning donde todas las posibles salidas de una señal de entrada son colocadas en cosets separados, o bins. En inglés bin significa depósito o recipiente, por lo que el termino binning se refiere a un proceso en el que la fuente es dividida (fragmentada) en diferentes muestras llamadas cosets o bins. En matemática un coset es un subconjunto que viene como resultado de la multiplicación de un elemento por todos los demás elementos de dicho conjunto. Esta teoría fue luego llamada “codificación de fuente distribuida usando síndromes” (DISCUS) en (Pradhan & Ramchandran, 2000, 2003).
Es fácil relacionar esta forma de codificación con un código de bloque binario lineal (k,n), el cual tendría 2^(n-k) síndromes distintos, cada uno indicando un bin de 2^k palabras binarias de longitud n (el símbolo ^ representa el valor de una potencia). Cada bin es un código coset del código de bloque binario lineal, preservando las propiedades de distancia Hamming del código lineal original en cada bin. De esta manera, una secuencia de n bits de entrada es mapeado dentro de sus correspondientes bits síndrome, logrando una razón de compresión de n:(n-k). Esta aproximación es conocida como “esquema Slepian-Wolf” (Xiong et al., 2004).
La codificación de fuente distribuida usando síndromes puede implementarse de varias formas dependiendo de la técnica de codificación del canal escogida. Las técnicas más comúnmente usadas en la codificación de fuente distribuida son los códigos de bloque lineales, los códigos convolucionales y los códigos concatenados. Sin embargo como la correlación entre las fuentes es entendida como un “canal virtual”, un código de canal que tenga una mejor capacidad correctora, en la codificación de fuente distribuida, ya necesita un menor grado de correlación entre las fuentes para obtener un mejor rendimiento en cuanto a la probabilidad de error.
Por tal motivo las investigaciones para la implementación de la codificación distribuida en las redes de sensores se han enfocado en la codificación LDPC y la codificación Turbo (Aaron & Girod, 2002; Bhattar, Ramakrishnan, & Dasgupta, 2010; Biroli, Martina, & Masera, 2012; Fresia, Vandendorpe, & Poor, 2009; Garcia-Frias, 2001; Garcia-Frias & Zhong, 2003; Lan, Liveris, Narayanan, Xiong, & Georghiades, 2004; Liveris, Xiong, & Georghiades, 2002; Sartipi & Fekri, 2008; Varodayan, Aaron, & Girod, 2005, 2006; Zamani & Lahouti, 2006; Zhao & Garcia-Frias, 2002). Ambos alcanzan rendimientos muy cercanos aunque con una relativa complejidad en comparación con el resto de los códigos de canal. Sin embargo los diseños LDPC son más flexibles y menos complejos, y por tanto más rápidos, fáciles y precisos. Esto ha hecho que los códigos LDPC sean los más investigados para la implementación de la codificación de fuente distribuida, aunque por su rendimiento también son sugeridos los códigos Turbo.
Cuando la Codificación de Fuente Distribuida implica la codificación de muchas fuentes a la vez se requiere el establecimiento de un modelo de correlación que sea aplicable a todas las fuentes involucradas. Aunque se han estudiado diferentes modelos de correlación para aplicaciones de redes de sensores específicas (Gray & Neuhoff, 1998; Lin & Costello, 1983; Servetto, 2000; A. D. Wyner & J. Ziv, 1976) en algunos casos se hace complejo llevar a la práctica algunas de estas aplicaciones y continuar utilizando una probabilidad conjunta masiva o una función de densidad en las redes de sensores especialmente si existen pocas áreas para probar o poca información acerca de la topología de la red.
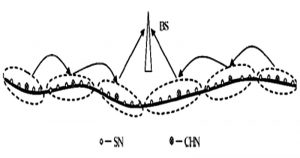
Determinar el modelo de correlación se dificulta aún más cuando la red ocupa una gran dimensión ya que su comportamiento difiere mucho entre los dispositivos de la red. Una alternativa muy empleada en las redes de sensores para mantener la correlación entre los nodos es fragmentar la red en clústeres de nodos correlacionados, donde cada clúster tiene un nodo padre y muchos nodos hijos (Xiong et al., 2004). Los nodos hijos envían la información comprimida a los nodos padres el cual procesa y/o retrasmite la información recolectada en el clúster a la estación base. Los clústeres se usan en redes de gran tamaño donde se hace difícil la correlación entre todos los nodos de la red y por tanto, lo más conveniente es en ese fragmentar la red en varios segmentos para facilitar la comunicación. Desde este enfoque es más viable implementar la estrategia asimétrica, de manera que los datos captados por el nodo padre son utilizados como la información lateral para decodificar la información de los nodos hijos en el clúster.
El primer acercamiento al despliegue de la codificación de fuentes distribuida en una red lo dio Han en (Han, 1980) donde se demuestra que las condiciones necesarias y suficientes para trasmitir fuentes correlacionadas en un enlace son definidas en la ecuación (2). Esta expresión expone que para poder trasmitir una fuente comprimida por la Codificación de Fuente Distribuida, en un enlace entre dos nodos i y j, la capacidad del canal debe ser mayor que la razón Ri, en la cual se codifico la fuente (y por tanto en la que se trasmiten los datos), para poder recuperar la fuente sin perdidas bajo ningún esquema. De igual modo para que la compresión se realice bajo los principios de la Codificación de Fuente Distribuida la razón de comprensión Ri tiene que estar dentro de los límites de Slepian-Wolf, es decir, siendo mayor o igual a la entropía condicional de las fuentes a codificar.
A partir de la ecuación (2), Li y Ramamoorthy en (Li & Ramamoorthy, 2011) analizan la optimización de la energía en la trasmisión desde el criterio de que la capacidad de un enlace entre un nodo i y un terminal dado puede ser escrito como la ecuación (3), desde donde se establece que la asignación de la energía optima puede ser escrita como la ecuación (4). De esta manera el problema de minimizar la suma de energía en la red puede ser definida como la ecuación (5).

En (5) se declara que la minimización de la energía total de la red usando la Codificación de Fuentes Distribuida está sujeta a las condiciones de que Ri este dentro de los límites de la región de Slepian-Wolf y la energía usada en la trasmisión en el nodo i tiene que ser menor que la energía residual de este nodo (Pmax). Como la menor razón de codificación Ri se obtiene en la estrategia asimétrica, explotando esta estrategia se obtiene el menor consumo de energía en la red. Sin embargo aunque se han realizado investigaciones para logar códigos que implementen la Codificación de Fuente Distribuida para múltiples fuentes, en la práctica solo se han podido logar códigos para dos fuentes.
Por tal razón los modelos que implementan la codificación de Selpian-Wolf en redes proponen, para imponer las restricciones anteriores, un modelo que llaman pairwise (en español significa: formar pares), para que dos fuentes puedan ser decodificadas de forma conjunta. Bajo este modelo, antes que la trasmisión comience, se determina el par de fuentes que son decodificadas juntas en cada tiempo y se determina las razones de las fuentes y los códigos correspondientes. Durante la trasmisión, las fuentes codifican los mensajes por separado (sin comunicación entre sí) usando el código pre-asignado y el terminal (o estación base de la red) realiza la decodificación conjunta a las combinaciones pre-asignadas. El problema de la asignación de recursos es para determinar las combinaciones pares óptimas y las razones para los sensores de forma que la suma de energía es minimizada.
Según Li y Ramamoorthy (2011) una asignación de la razón tiene la propiedad pairwise si permite que el terminal decodifique las fuentes en un modo pairwise. Específicamente, la asignación de la razón se dice que se satisface la propiedad pairwise si para cada fuente Xi, i = 1,…,N existe una secuencia ordenada de fuentes tal que se cumpla las inecuaciones: 6, 7 y 8.
Tal asignación de la razón admite la posibilidad de que cada fuente pueda ser reconstruida en el decodificador para resolver una secuencia de operaciones en el caso asimétrico de la codificación Slepian-Wolf. Como la menor razón (menor gasto de energía) se consigue en el caso asimétrico, la mayoría de los modelos pairwise propuestos se basan en este concepto.

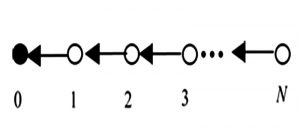
Un ejemplo claro es el presentado en (Guogang Hua, 2008), en el cual se propone un esquema de enrutamiento para la optimización de una topología de red tipo cadena, como se ilustra en la figura 4. En esta topología de red los nodos son desplegados de forma unidimensional. Para mantener la correlación entre los nodos, la red es segmentada en clústeres. La figura 5 representa un clúster dentro de la red. En su trabajo Guogang Hua propone un modelo pairwise que explota la estrategia asimétrica de la codificación de Slepian-Wolf, dentro de cada clúster, siguiendo el siguiente procedimiento:
- El nodo 1 codifica su información X1 a una razón de R1=H(X1|X0) y lo envía al nodo 0 (que tiene el rol de cabecera del clúster). Una suma de chequeo del dato original X1 es también enviado.
- El nodo 0 usa su información X0 como información lateral para con los bits del síndrome recibidos del nodo 1 tratar de decodificar X1. Después de la decodificación, el nodo 0 calcula la suma de chequeo de los datos decodificados. Si la suma de chequeo es la misma que la suma de chequeo de los datos decodificados, se asume que X1 fue recibido exitosamente por el nodo cabecera del clúster (CHN), de otra forma el CHN solicita al nodo 1 que le reenvié sus datos.
- El nodo 2 codifica sus datos a una razón de R2=H(X2|X1) y lo envía al nodo 0 a través del nodo 1. En este tiempo ya el nodo 0 debe tener la información del nodo 1 la cual utiliza como información lateral para decodificar los datos del nodo 2. Si un error ocurre le solicita al nodo 2 le reenvíe sus datos.
El proceso continúa para todos los nodos dentro del clúster. Por tanto todos los nodos pueden codificar su información a una razón de Rn=H(Xn|Xn-1) y enviarla al nodo cabecera.
Modelos pairwise similares al propuesto por Guogang Hua son propuestos en la literatura para diferentes esquemas de enrutamiento. No obstante, un criterio impórtante que se puede visualizar desde el método propuesto por Guogang Hua es que en algunos escenarios la Codificación de Fuente Distribuida no puede ser usada sin una adecuada sincronización entre los nodos de una red de sensores. Si no existe una correcta sincronización de los datos se corre el riesgo de que se produzca una decodificación errónea (o incluso que la decodificación no se logre realizar), ya que el decodificador necesita recibir la información de las fuentes que están correlacionadas entre sí de manera simultánea para poder reconstruir los datos de manera correcta. Esto quiere decir que varias suposiciones son hechas por los algoritmos de enrutamiento y cronometraje y sus respectivas concepciones en el diseño (Zixiang Xiong, Angelos D. Liveris, & Cheng, 2004). Por lo que encontrar un esquema que involucre tanto la codificación como el modelo de enrutamiento de la información en la red resulta una de las principales líneas de investigación en la actualidad.
Un principio primordial para optimizar el consumo de energía en el enrutamiento de las redes de sensores es la cooperación de los nodos para tramitar la información hasta la estación base, de modo que los nodos intermedios tienen que retrasmitir los datos de sus vecinos. Desde esta perspectiva el peso w de cada enlace entre nodo, desde el nodo fuente hasta el terminal, deben tenerse en cuenta para encontrar el camino más óptimo. Según (Cristescu, Beferull-Lozano, & Vetterli, 2005) el peso de un enlace entre los nodos es una función que depende de la distancia que separa los nodos. Por lo que el problema de la optimización puede ser escrito como la ecuación (9).
Si no hay restricción de capacidad, la solución del problema tiene una interpretación y forma simple. La idea básica es que en la ausencia de restricción de capacidad no existe necesidad de separar el flujo en diferentes enlaces. Una vez que una ruta desde la fuente dada al terminal con costo mínimo es encontrada, la fuente simplemente enruta todos los datos a través del camino. Como el peso del enlace está estrechamente relacionado con la distancia entre los nodos de ese enlace, el camino más óptimo es el que involucra las rutas más cortas (es decir la menor cantidad de saltos hasta el terminal, con los enlaces entre nodos de menor distancia). Sin embargo la elección de estas rutas también está sujetas a la energía residual que tengan los nodos, la cual tiene que ser suficiente para trasmitir los datos a la razón de codificación de Slepian-Wolf como establece la ecuación (5).
Si bien un esquema de enrutamiento que utilice los caminos más cortos desde la fuente al terminal y explote las propiedades de las estrategias de codificación asimétricas consigue el uso mínimo de la energía total de la red, no logra maximizar su tiempo de vida. Por una parte las estrategias asimétricas explotadas en los métodos pairwise hacen que los nodos más cercanos a la estación base actúen en la mayoría de los escenarios como proveedores de la información lateral, enviando sus datos sin codificar, por lo que el consumo de energía por este concepto será mayor que la del resto de los nodos en la red. Por otra parte, incluso si no tuvieran la función de proveer la información lateral, la sobrecarga relacionada con el enrutamiento de la información del resto de los nodos en la red es suficientemente significativa para que en estos nodos el tiempo de vida sea menor.
Para optimizar este parámetro en (Abughalieh et al., 2012) propone el uso de la codificación asimétrica conmutando periódicamente la razón de codificación entre los nodos, cada T intervalo de tiempo. Es decir, intercambiando el rol de proveer la información lateral para la decodificación de los datos.
Conclusiones
La Codificación de Fuentes Distribuida en las redes de sensores inalámbricos logra una considerable comprensión de los bits a trasmitir, explotando la correlación entre las fuentes de una forma no centralizada. La región de la razón de codificación de Selpian-Wolf presenta dos estrategias de codificación: asimétrica y simétrica, siendo la primera idónea para optimizar la eficiencia energética en las redes. Sin embargo, la función de proveedor de la información lateral debe ser intercambiada entre los nodos periódicamente para maximizar el tiempo de vida de la red. La no existencia de códigos de codificación distribuida que puedan aplicarse para múltiples fuentes a la vez, hacen que los métodos pairwise deban ser considerados a la hora de implementar esta técnica en las redes, teniendo en cuenta la sincronización entre los nodos. Un principio imprescindible para la aplicación de la Codificación de Fuente Distribuida es el mantenimiento del modelo de correlación, para el cual los protocolos de enrutamiento jerárquicos que segmenten la red en clústeres, basados en la distribución espacial de la correlación, son la mejor alternativa para enfrentar este problema. Referencias Bibliográficas Aaron, A. & Girod, B. (2002). Compression with side information using turbo codes. Paper presented at the Data Compression Conference. Proceedings. DCC. Abughalieh, N., Steenhaut, K., Lemmens, B. & Nowé, A. (2012). A Mutual Algorithm for Optimizing Distributed Source Coding in Wireless Sensor Networks International Journal of Distributed Sensor Networks. Arjmandi, H. & Lahouti, F. (2011). Resource optimized distributed source coding for complexity constrained data gathering wireless sensor networks. IEEE Sensors Journal, 11, no. 9, 2094–2101. Arjmandi, H., Taki, M. & Lahouti, F. (2011). Lifetime maximized data gathering in wireless sensor networks using limited-order distributed source coding. Signal Processing, 91, no. 11, 2661–2666. Bhattar, R. K., Ramakrishnan, K. & Dasgupta, K. (2010). Density Evolution Technique for LDPC Codes in Slepian-Wolf Coding of Nonuniform Sources. International Journal of Computer Applications IJCA, 7(8), 1-7. Biroli, A. D. G., Martina, M. & Masera, G. (2012). An ldpc decoder architecture for wireless sensor network applications. Sensors, 12(2), 1529-1543. Cristescu, R., Beferull-Lozano, B. & Vetterli, M. (2005). Networked Slepian–Wolf: Theory, Algorithms, and Scaling Laws (2005). IEEE Transactions on Information Theory, 51. No. 12. Dargie, W. & Poellabauer, C. (2010). Fundamentals of wireless sensor networks: John Wiley & Sons Ltd. Fresia, M., Vandendorpe, L. & Poor, H. V. (2009). Distributed source coding using raptor codes for hidden markov sources. Signal Processing, IEEE Transactions on, 57(7), 2868-2875. Garcia-Frias, J. (2001). Compression of correlated binary sources using turbo codes. Communications Letters, IEEE, 5(10), 417-419. Garcia-Frias, J. & Zhong, W. (2003). LDPC codes for compression of multi-terminal sources with hidden Markov correlation. IEEE Communications Letters, 7(3), 115-117. Gray, R. & Neuhoff, D. ( 1998). Quantization. EEE Trans. Inform. Theory, 44, 2325-2382. Guogang Hua, C. W. C. (2008). Correlated data gathering in wireless sensor networks based on distributed source coding Int. J. Sensor Networks, 4 Nos. 1/2. Han, T. (1980). Slepian-Wolf-Cover theorem for network of channels. INFO. AND CONTR., 47(1), 67-83. Lan, C.-F., Liveris, A. D., Narayanan, K., Xiong, Z. & Georghiades, C. (2004). Slepian-Wolf coding of multiple M-ary sources using LDPC codes. Paper presented at the Data Compression Conference. Proceedings. DCC. Li, S. & Ramamoorthy, A. (2011). Networked distributed source coding Theoretical Aspects of Distributed Computing in Sensor Networks (pp. 191-224): Springer. Lin, S., & Costello, D. (1983). Error Control Coding: Fundamentals and Applications. Liveris, A. D., Xiong, Z., & Georghiades, C. N. (2002). Compression of binary sources with side information at the decoder using LDPC codes. Communications Letters, IEEE, 6(10), 440-442. Pradhan, S. S., & Ramchandran, K. (2000). Distributed source coding: Symmetric rates and applications to sensor networks. Paper presented at the Data Compression Conference, 2000. Proceedings. DCC 2000. Pradhan, S. S. & Ramchandran, K. (2003). Distributed source coding using syndromes (DISCUS): Design and construction. Information theory, IEEE Transactions on, 49(3), 626-643. Sartipi, M. & Fekri, F. (2008). Distributed source coding using short to moderate length rate-compatible LDPC codes: the entire Slepian-Wolf rate region. Communications, IEEE Transactions on, 56(3), 400-411. Servetto, S. (2000). Lattice quantization with side information. Proc. DCC’OO, Snowbird, UT. Slepian, D., & Wolf, J. K. (1973). Noiseless coding of correlated information sources. Information theory, IEEE Transactions on, 19(4), 471-480. Stankovic, V., Stankovic, L., & Cheng, S. (2010). Distributed source coding: Theory and applications. Paper presented at the Signal Processing Conference, 2010 18th European. Tubaro, S. & Vetro, A. (2013). Distributed Video Coding. Hindawi. Varodayan, D., Aaron, A. & Girod, B. (2005). Rate-adaptive distributed source coding using low-density parity-check codes. Paper presented at the Proc. Asilomar Conf. on Signals, Syst., Comput., Pacific Grove, CA. Varodayan, D., Aaron, A. & Girod, B. (2006). Rate-adaptive codes for distributed source coding. Signal Processing, 86(11), 3123-3130. Wyner, A. D. (1978). The rate-distortion function for source coding with side information at the decoder\ 3-II: General sources. Information and control, 38(1), 60-80. Wyner, A. D. & Ziv, J. (1976). The rate-distortion function for source coding with side information at the decoder. Information theory, IEEE Transactions on, 22(1), 1-10. Wyner, A. D. & Ziv, J. (1976). The Rate-Distortion Function for Source Coding with Side Information at the Decoder. IEEE Transactions on Information Theory, IT-22. Xiong, Z., Liveris, A. D. & Cheng, S. (2004). Distributed source coding for sensor networks. Signal Processing Magazine, IEEE, 21(5), 80-94. Zamani, M. & Lahouti, F. (2006). Distributed source coding using symbol-based turbo codes. Paper presented at the Communications, 23rd Biennial Symposium on. Zhao, Y. & Garcia-Frias, J. (2002). Data compression of correlated non-binary sources using punctured turbo codes. Paper presented at the Data Compression Conference. Proceedings. DCC. Zixiang, X., Angelos, D., Liveris & Cheng, S. (2004). Distributed Source Coding for Sensor Networks. IEEE Signal processing.