Herramienta Solver para la toma de decisiones

Solver tool for decision making

Autor: Mario Abel Vega Vega / mario.vega@ltu.jovenclub.cu

Resumen: Solver es una herramienta de Microsoft Excel y OpenOffice.org Calc que facilita la toma de decisiones al resolver problemas de optimización a partir  de los recursos (materiales, humanos, tecnológicos, de tiempo, etc) disponibles en una entidad. Con Solver puede definir, por ejemplo  la cantidad de artículos de cada tipo a producir para minimizar costos o maximizar las ganancias; cantidad de ingredientes a utilizar para la elaboración de pienso animal con los requerimientos alimenticios necesarios; disminución de desechos; la distribución optima de recursos de un origen  a varios destinos, entre otras decisiones administrativas. 

Abstract: Solver is a Microsoft Excel and OpenOffice.org Calc tool that facilitates decision making when solving optimization problems based on the resources (material, human, technological, time, etc.) available in an entity. With Solver you can define, for example, the number of items of each type to produce to minimize costs or maximize profits; quantity of ingredients to be used for the elaboration of animal feed with the necessary nutritional requirements; waste reduction; the optimal distribution of resources from one origin to several destinations, among other administrative decisions.

Palabras claves:  Microsoft Excel, Solver, Optimización, Programación lineal

Introducción

El desarrollo impetuoso  de las Nuevas Tecnologías de la Información y la Comunicación ofrece un sin número de posibilidades para logar este objetivo. La herramienta Solver de Microsoft Excel y OpenOffice.org Calc es útil en este propósito al  resolver problemas de optimización.

Ejemplo de problemas que se pueden resolver utilizando Solver:

• ¿Cuántas unidades del producto  A y cuántas de B deben fabricarse para obtener un beneficio máximo?
• ¿Cuántas unidades del producto  A y cuántas de B deben fabricarse para minimizar los costos?
• ¿Cuántas unidades del producto  A y cuántas de B deben fabricarse para maximizar la producción bruta?
• ¿Cuántas rastras de tipo A, B y C  deberá comprar una empresa de trasporte de carga, si se desea hacer máxima su capacidad ton.Km?
• ¿Qué cantidad de alimento M y N se debe utilizar diariamente por cabeza de ganado para realizar una alimentación adecuada y menos costosa?
• ¿Cómo deben cortarse las planchas  de cartón  para surtir el pedido con el mínimo de desperdicios?.
• ¿Cómo distribuir el producto A que elabora una empresa en  tres fábricas distantes para abastecer  a cuatro clientes de tal forma que se  minimice el costo de transporte?
• Cómo seleccionar 4 personas de  5 para  operar 4 máquinas diferentes?

Desarrollo

Investigación de operaciones

La investigación de operaciones es una rama de la administración que consiste en el uso de modelos matemáticos para el estudio de complejos sistemas reales, con la finalidad de mejorar (u optimizar) su funcionamiento teniendo en cuenta las restricciones en los recursos materiales, humanos, tecnológicos, de tiempo, etc, para determinar cómo se puede logar un objetivo con la maximización de los beneficios o la minimización de costos.

Entre las  técnicas de la Investigación de operaciones se encuentran:

1. Programación lineal
2. Programación no lineal
3. Programación multicriterio
4. Programación por Metas
5. Teoría de inventarios
6. Fenómenos de espera
7. Teoría de las decisiones
8. Teoría de juegos
9. Teoría de redes

Modelo Matemático de programación lineal

Dada una función lineal de varias variables, se quieren determinar valores no negativos para dichas variables que maximizan o minimicen el valor de la función lineal, sujeta a cierto número de limitaciones.

Hallar los valores de x_J  que hagan máximo o mínimo el valor de la función lineal (Función objetivo).

Para cada restricción se utiliza uno solo de los signos;

x_j – Variables de decisión (variables a optimizar)

c_j – Coeficientes económicos

a_ij – Coeficientes tecnológicos

b_j  – Termino independiente

Donde

• Variables de decisión: Incógnitas del modelo, lo que se busca con la solución del mismo. Actividades o productos que compiten por los recursos materiales, técnicos, tiempo disponible, etc.
• Coeficientes económicos: Coeficientes de la función objetivo para cada actividad o producto. Contribución de cada variable de decisión a la función objetivo, como por ejemplo, ganancia o costo por unidad de producto.
• Coeficientes tecnológicos: Coeficientes de parte izquierda de las  restricciones: Representan, por ejemplo, unidades de  un recurso necesarias para producir una unidad de un producto, horas de tiempo de troquelado por tipo de materiales a troquelar, horas en horno por unidad de pieza a  fundir, etc.
• Términos independientes: Términos de la parte derecha de las  restricciones: Representan la disponibilidad  o demanda de los recursos, como por ejemplo, horas-hombre, horas-máquina, espacio, dinero, materia prima, requerimientos de calidad, capacidad de producción, cantidad máxima o mínima, etc.

La expresión (1.3) expresa el requerimiento de que las variables, sean no negativas y  se denomina condición de no negatividad.

Solución de problemas de programación lineal con Solver

Solver es una herramienta de Microsoft Excel yOpenOffice.org Calcque permite resolver problemas de optimización, es decir, a partir de un objetivo y estableciendo unas condiciones (restricciones), se puede buscar el valor óptimo para una celda, denominada celda objetivo, en donde se escribe la fórmula de la función objetivo f (x₁, x₂, …, x_n).

Solver cambia los valores de un grupo de celdas, denominadas variables de decisión  y que estén relacionadas, directa o indirectamente, con la fórmula de la celda objetivo. En estas celdas se encuentran los valores de las variables controlables x₁, x₂, …, x_n.

Solver ajusta los valores en las celdas de variables de decisión para cumplir con los límites en las celdas de restricción y producir el resultado deseado para la celda objetivo.

Nota: Si la herramienta Solver no está disponible en la pestaña Datos de Microsoft Excel deberá cargar el programa de complemento.

Siga los siguientes pasos para resolver  problemas de programación lineal con Solver

1. Planteé  el problema en lenguaje matemático
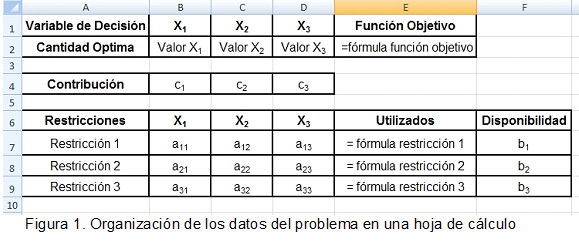
2. Organice los datos del problema en una hoja de Excel o OppenOffice  Calc

Ejemplo

• En Datos, haga clic en Solver.
• En el cuadro Establecer objetivo, escriba una referencia de celda o un nombre para la celda objetivo. La celda objetivo debe contener una fórmula vinculada a las variables de decisión (celda =fórmula función objetivo).
• Siga uno de los procedimientos siguientes:
• Si desea que el valor de la celda objetivo sea el valor máximo posible, haga clic en Máximo.
• Si desea que el valor de la celda objetivo sea el valor mínimo posible, haga clic en Mínimo.
• Si desea que la celda objetivo tenga un valor determinado, haga clic en Valor de y luego escriba el valor en el cuadro.
• En el cuadro Cambiando las celdas, escriba un nombre o una referencia para cada rango de celda de las variables de decisión (celdas Valor X_1, Valor X_1, Valor X_1, etc). Separe con comas las referencias no adyacentes. Las celdas de variables deben estar directa o indirectamente relacionadas con la celda objetivo.
• En el cuadro Sujeto a las restricciones, realice lo siguiente para especificar todas las restricciones que desee aplicar.
• Haga clic en Agregar.
• En el cuadro Referencia de la celda, escriba la referencia de celda o el nombre del rango de celdas para los que desea restringir el valor. (En la columna Utilizados las  celdas= fórmula restricción i)
• Haga clic en la relación (<=, =, >=, int o bin) que desea establecer entre la celda a la cual se hace referencia y la restricción.

Si hace clic en int, aparece integer en el cuadro Restricción. Si hace clic en bin, aparece binary en el cuadro Restricción.

Si elige <=, =, o >= para la relación en el cuadro Restricción, escriba un número, una referencia de celda o nombre o una fórmula.

• En el cuadro Restricción escriba la referencia de celda o el nombre del rango de celdas de la disponibilidad del recurso. (En la columna Disponibilidad las  celdas= bi)
• Siga uno de los procedimientos siguientes:

1. Para aceptar una restricción y agregar otra, haga clic en Agregar.
2. Para aceptar la restricción y volver al cuadro de diálogo Parámetros de Solver, haga clic en Aceptar.
3. Hagas clic en Opciones y  seleccione la casilla Adoptar modelo lineal. Seleccione la casilla Adoptar no negativos si desea que todos los valores de las  celdas  cambiantes  sean  ≥  0.  
4. Haga clic en Resolver y siga uno de los procedimientos siguientes:

• Para mantener los valores de la solución en la hoja de cálculo, en el cuadro de diálogo Resultados de Solver, haga clic en Conservar solución de Solver.
• Para restaurar los valores originales tal como estaban antes de hacer clic en Resolver, haga clic en Restaurar valores originales.

Solver genera tres informes para programas lineales.

• Informe de Respuestas: Informe de Solver que  proporciona el valor inicial y final de la celda objetivo y de todas las celdas cambiantes, así como un listado de cada restricción  y  su  estado.
• Informe de Sensibilidad (Confidencialidad en Excel 2010): Informe de Solver que  proporciona el valor óptimo de cada celda cambiante, su coste reducido, el  coeficiente  de  función  objetivo y el aumento y la disminución de éste para el cual la solución en curso permanece óptima (el resto permanece fijo).
• Informe límites: Informe de Solver que  da los límites superior e inferior de cada celda cambiante manteniendo el resto de las celdas ajustables en su valor actual y cumpliendo las restricciones.

Conclusiones

Con  Solver es posible resolver problemas  de optimización con los recursos disponibles en una entidad,  lo que lo convierte en una herramienta informática de gran valor para  la toma de decisiones y el logro de la eficiencia y eficacia de los procesos productivos y de servicio.

Referencias Bibliográficas

Charles A. G.  y Hugh J. W. (1982). Métodos cuantitativos para la toma de decisiones en administración. México.  McGRAW-HILL.

Colectivo de Autores (2008) Métodos cuantitativos para administración México. McGRAW-HILL/INTERAMERICANA EDITORES.

Colectivo de Autores (s/a).  Métodos cuantitativos para los negocios México. CENGAGE LEARNING

Eppen, G. D (2000). Investigación de Operaciones en la Ciencia Administrativa. Construcción de Modelos para la toma de Decisiones con Hojas de Cálculo Electrónicas. México.  PRENTICE-HALL.

Frederick S. H. y Gerald J. L. (2010).   Introducción a la investigación de operaciones. México.  McGRAW-HILL/INTERAMERICANA EDITORES, S. A.

Hamdy, A. T. (2012) Investigación de operaciones. México. PERARSON EDUCACIÓN.

Render, B. (2012) Métodos cuantitativos para los negocios. México.  PEARSON EDUCACIÓN.

Wayne, L. W. (2005). Investigación de operaciones. Aplicaciones y Algoritmos México. THOMSON.

Enlaces relacionados

¿Cómo enlazar documentos de Excel con documentos de Word? en el Número 53 de Tino

¿Celdas inteligentes en Microsft Excel? en el Número 49 de Tino